Blender2.5x-2.6完全教程 3.4.2:修订间差异
来自Ubuntu中文
跳到导航跳到搜索
| (未显示同一用户的22个中间版本) | |||
| 第1行: | 第1行: | ||
=第 3.4.2 节 聚合点线面 (merge)= | =第 3.4.2 节 聚合点线面 (merge)= | ||
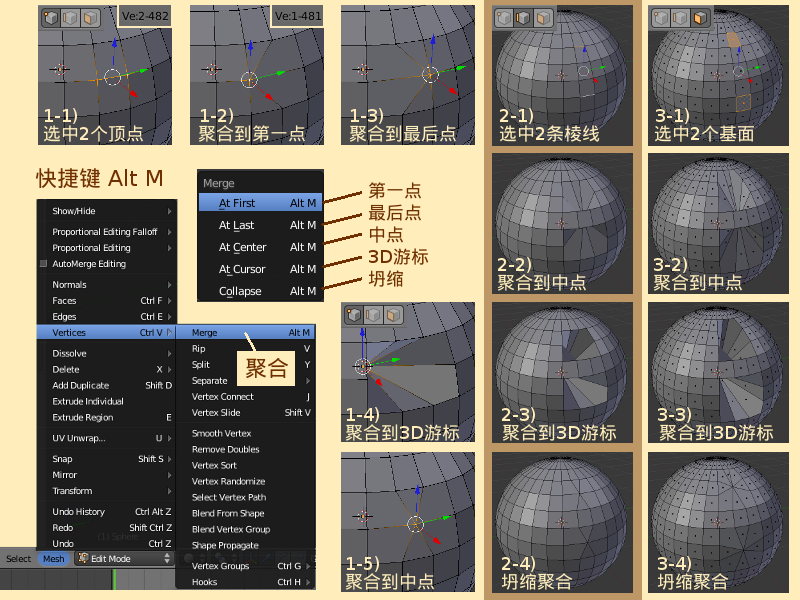
在Edit编辑模式下,Mesh网格菜单的Vertex顶点子菜单中,有一个Merge聚合命令(快捷键 Alt | 在Edit编辑模式下,Mesh网格菜单的Vertex顶点子菜单中,有一个Merge聚合命令(快捷键 Alt M),在左侧Tool Shelf工具栏的Mesh网格栏目的Remove移除项目下,也有Merge聚合按钮,其作用是Merge selected vertices聚合已选中的顶点,也就是说,把多个顶点聚拢并融合为一个。而这个聚拢的方式,在执行Merge聚合命令时,会弹出一个菜单,或者在执行Merge聚合命令之后,左侧Tool Shelf工具栏下方的Merge聚合栏目里,有一个Type类型菜单,和执行Merge聚合命令时弹出的菜单一模一样,用于Merge method to use选择聚合的方式。有以下几种可选: | ||
{| align=center border=0 style="width: 50%;" | {| align=center border=0 style="width: 50%;" | ||
| 第23行: | 第23行: | ||
|- bgcolor=#FFDDAA | |- bgcolor=#FFDDAA | ||
| Collapse | | Collapse | ||
| | | 坍缩聚合 | ||
| | | (仅对棱线和基面有效) | ||
|} | |} | ||
*View视图里默认已有并已选中Cube立方体 ⇒ X 删除,回车确认 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ UV Sphere 经纬球 ⇒ Tab 切换到Edit编辑模式 ⇒ A 全不选 ⇒ 按着Shift键不放,鼠标右键点击选中相邻的2个顶点 ⇒ 此时最后选中的顶点是白色的活动顶点 ⇒ 注意看上方Info信息编辑器里显示着Ve:2-482 共有482个顶点,已选中2个 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At First聚合到第一点 ⇒ 可以看到,2个顶点聚合在了一起,聚合的位置是之前第一个被选中的顶点的位置 ⇒ 注意看上方Info信息编辑器里显示着Ve:1-481 共有481个顶点,已选中1个,由此可知2个顶点已经被融合为了一个 | *View视图里默认已有并已选中Cube立方体 ⇒ X 删除,回车确认 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ UV Sphere 经纬球 ⇒ Tab 切换到Edit编辑模式 ⇒ A 全不选 ⇒ 按着Shift键不放,鼠标右键点击选中相邻的2个顶点 ⇒ 此时最后选中的顶点是白色的活动顶点 ⇒ 注意看上方Info信息编辑器里显示着Ve:2-482 共有482个顶点,已选中2个 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At First聚合到第一点 ⇒ 可以看到,2个顶点聚合在了一起,聚合的位置是之前第一个被选中的顶点的位置 ⇒ 注意看上方Info信息编辑器里显示着Ve:1-481 共有481个顶点,已选中1个,由此可知2个顶点已经被融合为了一个 | ||
*继续上例 ⇒ | *继续上例 ⇒ 左侧Tool Shelf工具栏下方的Merge聚合栏目 ⇒ 在Type类型菜单中,选择At Last则聚合到最后选中的顶点 ⇒ 选择At Center则聚合到已选中的顶点的共同中心点,'''注意:这个中心点是2个顶点在三维坐标的中心点,不是“2个顶点在球体表面的中心点”''' ⇒ 选择At Cursor则聚合到3D游标所在的位置(本例即是在经纬球的中心) ⇒ 如果选中的是2个以上的多个顶点,则这三种Merge聚合方式产生的效果也是类似的。 | ||
由于本例选中的是2个相邻的顶点,这也等于是一条棱线,所以选择Collapse坍缩时,棱线的2端都会聚合到棱线的中央,这的效果等同于At Center聚合到中点。'''但如果选中的是2个不相邻的顶点,那么Collapse坍缩的聚合方式则不会起到任何作用。'''因为一个单独的顶点已经是最小的元素了,所以不可能再Collapse坍缩聚合,只有棱线或基面才可以Collapse坍缩聚合。 | |||
*继续上例 ⇒ Ctrl Tab 2 切换为棱线选取模式(请参考[[Blender2.5x-2.6完全教程_3.1.2|第 3.1.2 节]]) ⇒ 按着Shift键不放,鼠标右键点击选中2条不相邻的棱线 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,2条棱线在它们的中央聚合了。注意:这个中心点是2条棱线三维坐标的中心点,不是“2条棱线球体表面的中心点” ⇒ 左侧Tool Shelf工具栏下方的Merge聚合栏目 ⇒ 在Type类型菜单中,选择Collapse坍缩聚合,可以看到2条棱线在它们各自的位置上各自Collapse坍缩聚合,2条棱线变成了2个顶点,这与At Center把2条棱线聚合成一个顶点有所不同。 | |||
[[Image:Blender-tutorial_3-4-2_01.png]] | |||
巧妙地利用Merge聚合命令,可以很方便地创造出一些有趣的造型。 | |||
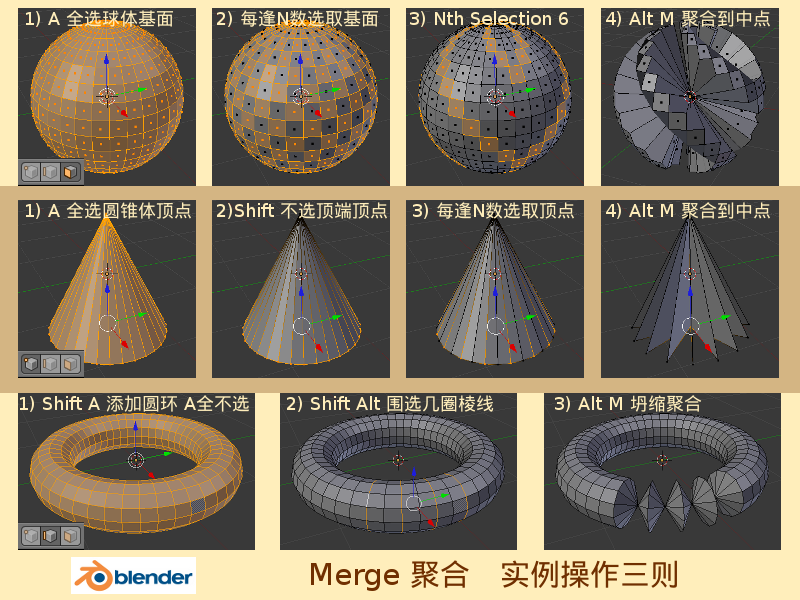
*继续上例 ⇒ 按几次Ctrl Z 回到一个完整的球体状态(或者按Alt Ctrl Z 在操作历史记录中选择回到一个完整的球体状态,请参考[[Blender2.5x-2.6完全教程_2.1.2|第 2.1.2 节]]) ⇒ Ctrl Tab 3 切换为基面选取模式 ⇒ A 全选全部基面 ⇒ 视图下方的Select选择菜单 ⇒ Every N Number of Verts 每逢N数选取顶点 ⇒ 左侧Tool Shelf工具栏下方Select Nth 逢N选取栏目 ⇒ 调节其中的Nth Selection逢N选取项目参数为6(请参考[[Blender2.5x-2.6完全教程_3.2.6|第 3.2.6 节]]) ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,球体变成了一朵由几圈曲面组成的花朵。 | |||
*继续上例 ⇒ A A 全不选,然后全选 ⇒ X 删除,选择Vertices删除顶点 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ 在菜单中选择Cone圆锥体 ⇒ 默认已经全选,按着Shift键鼠标右键点击圆锥体顶部的顶点,取消顶点的选择 ⇒ 视图下方的Select选择菜单 ⇒ Every N Number of Verts 每逢N数选取顶点 ⇒ 左侧Tool Shelf工具栏下方Select Nth 逢N选取栏目 ⇒ 调节其中的Nth Selection逢N选取项目参数默认为2保持不变 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,圆锥体变成了由许多三角形叶片组成的塔形。 | |||
*继续上例 ⇒ A A 全不选,然后全选 ⇒ X 删除,选择Vertices删除顶点 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ 在菜单中选择最后一项Torus圆环 ⇒ A 全不选 ⇒ Ctrl Tab 2 切换为棱线选取模式 ⇒ 按着Shift键和Alt键不放,鼠标右键点击Loop围选一圈'''纵向'''的棱线(请参考[[Blender2.5x-2.6完全教程_3.2.2|第 3.2.2 节]]) ⇒ 同样的方法,间隔一些距离围选几圈纵向的棱线 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择Collapse坍缩聚合,可以看到这几圈围选的棱线收缩起来,整个圆环形成了一串宝石的样子。 | |||
[[Image:Blender-tutorial_3-4-2_02.png]] | |||
在Edit编辑模式View视图下方Mesh网格菜单里,还有一个AutoMerge Editing编辑时自动聚合,勾选之后,就可以在编辑时自动把位置重合的顶点融合为一,详细的使用方法请参考[[Blender2.5x-2.6完全教程_3.3.5|第 3.3.5 节]]。 | |||
===<center>— [[Blender2.5x-2.6完全教程|返回目录]] —</center>=== | ===<center>— [[Blender2.5x-2.6完全教程|返回目录]] —</center>=== | ||
2012年9月4日 (二) 09:50的最新版本
第 3.4.2 节 聚合点线面 (merge)
在Edit编辑模式下,Mesh网格菜单的Vertex顶点子菜单中,有一个Merge聚合命令(快捷键 Alt M),在左侧Tool Shelf工具栏的Mesh网格栏目的Remove移除项目下,也有Merge聚合按钮,其作用是Merge selected vertices聚合已选中的顶点,也就是说,把多个顶点聚拢并融合为一个。而这个聚拢的方式,在执行Merge聚合命令时,会弹出一个菜单,或者在执行Merge聚合命令之后,左侧Tool Shelf工具栏下方的Merge聚合栏目里,有一个Type类型菜单,和执行Merge聚合命令时弹出的菜单一模一样,用于Merge method to use选择聚合的方式。有以下几种可选:
| At First | 聚合到第一点 | (仅对顶点有效) |
| At Last | 聚合到最后点 | (仅对顶点有效) |
| At Center | 聚合到中点 | |
| At Cursor | 聚合到3D游标 | |
| Collapse | 坍缩聚合 | (仅对棱线和基面有效) |
- View视图里默认已有并已选中Cube立方体 ⇒ X 删除,回车确认 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ UV Sphere 经纬球 ⇒ Tab 切换到Edit编辑模式 ⇒ A 全不选 ⇒ 按着Shift键不放,鼠标右键点击选中相邻的2个顶点 ⇒ 此时最后选中的顶点是白色的活动顶点 ⇒ 注意看上方Info信息编辑器里显示着Ve:2-482 共有482个顶点,已选中2个 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At First聚合到第一点 ⇒ 可以看到,2个顶点聚合在了一起,聚合的位置是之前第一个被选中的顶点的位置 ⇒ 注意看上方Info信息编辑器里显示着Ve:1-481 共有481个顶点,已选中1个,由此可知2个顶点已经被融合为了一个
- 继续上例 ⇒ 左侧Tool Shelf工具栏下方的Merge聚合栏目 ⇒ 在Type类型菜单中,选择At Last则聚合到最后选中的顶点 ⇒ 选择At Center则聚合到已选中的顶点的共同中心点,注意:这个中心点是2个顶点在三维坐标的中心点,不是“2个顶点在球体表面的中心点” ⇒ 选择At Cursor则聚合到3D游标所在的位置(本例即是在经纬球的中心) ⇒ 如果选中的是2个以上的多个顶点,则这三种Merge聚合方式产生的效果也是类似的。
由于本例选中的是2个相邻的顶点,这也等于是一条棱线,所以选择Collapse坍缩时,棱线的2端都会聚合到棱线的中央,这的效果等同于At Center聚合到中点。但如果选中的是2个不相邻的顶点,那么Collapse坍缩的聚合方式则不会起到任何作用。因为一个单独的顶点已经是最小的元素了,所以不可能再Collapse坍缩聚合,只有棱线或基面才可以Collapse坍缩聚合。
- 继续上例 ⇒ Ctrl Tab 2 切换为棱线选取模式(请参考第 3.1.2 节) ⇒ 按着Shift键不放,鼠标右键点击选中2条不相邻的棱线 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,2条棱线在它们的中央聚合了。注意:这个中心点是2条棱线三维坐标的中心点,不是“2条棱线球体表面的中心点” ⇒ 左侧Tool Shelf工具栏下方的Merge聚合栏目 ⇒ 在Type类型菜单中,选择Collapse坍缩聚合,可以看到2条棱线在它们各自的位置上各自Collapse坍缩聚合,2条棱线变成了2个顶点,这与At Center把2条棱线聚合成一个顶点有所不同。
巧妙地利用Merge聚合命令,可以很方便地创造出一些有趣的造型。
- 继续上例 ⇒ 按几次Ctrl Z 回到一个完整的球体状态(或者按Alt Ctrl Z 在操作历史记录中选择回到一个完整的球体状态,请参考第 2.1.2 节) ⇒ Ctrl Tab 3 切换为基面选取模式 ⇒ A 全选全部基面 ⇒ 视图下方的Select选择菜单 ⇒ Every N Number of Verts 每逢N数选取顶点 ⇒ 左侧Tool Shelf工具栏下方Select Nth 逢N选取栏目 ⇒ 调节其中的Nth Selection逢N选取项目参数为6(请参考第 3.2.6 节) ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,球体变成了一朵由几圈曲面组成的花朵。
- 继续上例 ⇒ A A 全不选,然后全选 ⇒ X 删除,选择Vertices删除顶点 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ 在菜单中选择Cone圆锥体 ⇒ 默认已经全选,按着Shift键鼠标右键点击圆锥体顶部的顶点,取消顶点的选择 ⇒ 视图下方的Select选择菜单 ⇒ Every N Number of Verts 每逢N数选取顶点 ⇒ 左侧Tool Shelf工具栏下方Select Nth 逢N选取栏目 ⇒ 调节其中的Nth Selection逢N选取项目参数默认为2保持不变 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择At Center聚合到中点,可以看到,圆锥体变成了由许多三角形叶片组成的塔形。
- 继续上例 ⇒ A A 全不选,然后全选 ⇒ X 删除,选择Vertices删除顶点 ⇒ Shift A 添加 ⇒ Mesh 网格物体 ⇒ 在菜单中选择最后一项Torus圆环 ⇒ A 全不选 ⇒ Ctrl Tab 2 切换为棱线选取模式 ⇒ 按着Shift键和Alt键不放,鼠标右键点击Loop围选一圈纵向的棱线(请参考第 3.2.2 节) ⇒ 同样的方法,间隔一些距离围选几圈纵向的棱线 ⇒ Alt M 聚合 ⇒ 在弹出的菜单中选择Collapse坍缩聚合,可以看到这几圈围选的棱线收缩起来,整个圆环形成了一串宝石的样子。
在Edit编辑模式View视图下方Mesh网格菜单里,还有一个AutoMerge Editing编辑时自动聚合,勾选之后,就可以在编辑时自动把位置重合的顶点融合为一,详细的使用方法请参考第 3.3.5 节。